Even though you made sure your computer was installed with the hottest technology, all the excitement will be over once you try to calculate the 40th Fibonacci number. The guy has been gone for almost 800 years but his famous sequence is still making 21st-century micro chips struggle. Well done, Leo. You win.

Whenever a function needs to re-run some calculations that have already been made, memoization comes to the rescue. It is basically a way to remember the solution to a problem so the same calculation doesn't have to be run over and over. It's easy and highly efficient; a sort of caching the return value of a function with a specific argument so we can use it later at a fast speed.

Here, we have a rather simple use-case of memorization.

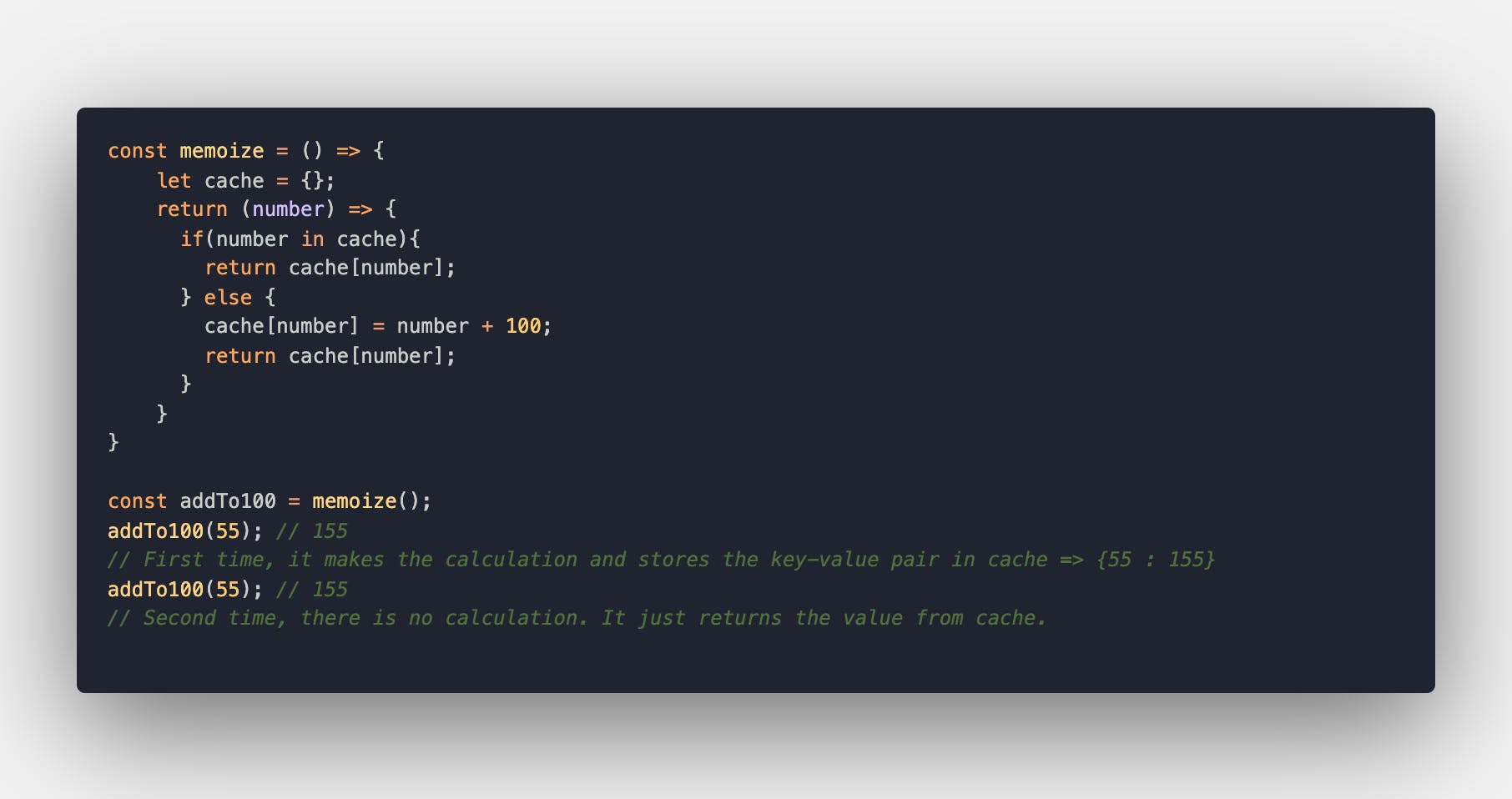
Combining closures and a cache-like object to store every new result, we can now skip calculating number + 100 every time addTo100 is invoked, but only the first time that particular argument is passed.

Let's take a look at a more realistic scenario. Finding the n Fibonacci using recursion requires expensive function calls and repetitive calculations.

Not a big deal if n is small. But when we try to go higher than 35... well, that's a different story. Memoization can drastically improve efficiency by storing the results and returning the values when the same inputs occur again.

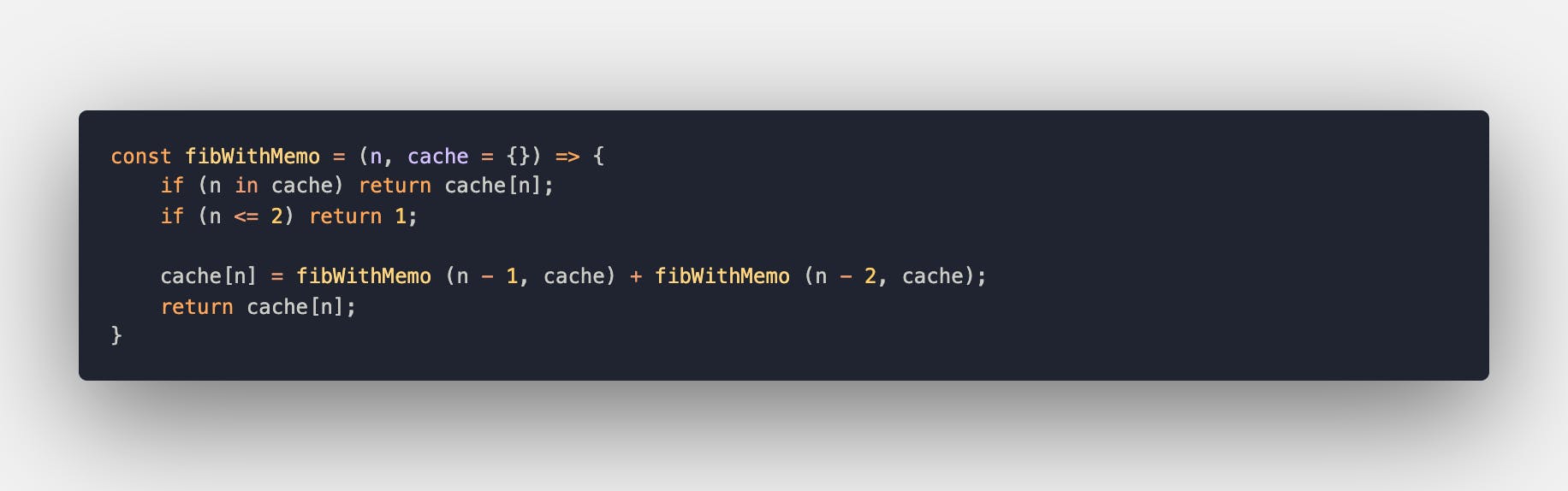
Now, every time the function receives an argument previously passed, the value is immediately returned from the cache object!

The speed difference is just amazing. A real performance game-changer.